파이썬으로 데이터 분석하기 #4-1

파이썬 기반 데이터 분석 환경에서 NumPy는 행렬 연산을 위한 핵심 라이브러리입니다. NumPy는 “Numerical Python”의 약자로 대규모 다차원 배열과 행렬 연산에 필요한 다양한 함수를 제공합니다. 특히 메모리 버퍼에 배열 데이터를 저장하고 처리하는 효율적인 인터페이스를 제공합니다. 파이썬 list 객체를 개선한 NumPy의 ndarray 객체를 사용하면 더 많은 데이터를 더 빠르게 처리할 수 있습니다.

배열 만들기

import numpy as np

# 1차원 배열
arr = np.array([1, 2, 3])
arr

>>> array([1, 2, 3])

# 2차원 배열
arr2 = np.array([[1, 2, 3], [4, 5, 6]])
arr2

>>>
array([[1, 2, 3],
       [4, 5, 6]])

# 3차원 배열
arr3 = np.array([[[1,2,3], [4,5,6]], [[3,2,1], [4,5,6]]])
arr3

>>>

array([[[1, 2, 3],
        [4, 5, 6]],

       [[3, 2, 1],
        [4, 5, 6]]])

배열 생성 및 초기화

# zeros((행, 열)) : 0으로 채우는 함수
arr_zeros = np.zeros((3,4))
arr_zeros

>>>
array([[0., 0., 0., 0.],
       [0., 0., 0., 0.],
       [0., 0., 0., 0.]])

# ones((행, 열)) : 1로 채우는 함수
arr_ones = np.ones((2,2))
arr_ones

>>>
array([[1., 1.],
       [1., 1.]])

# full((행, 열), 값) : 값으로 채우는 함수
arr_full = np.full((3, 4), 7)
arr_full

>>>
array([[7, 7, 7, 7],
       [7, 7, 7, 7],
       [7, 7, 7, 7]])

# eye(N) : (N, N)의 단위 행렬 생성
arr_eye = np.eye(5)
arr_eye

>>>
array([[1., 0., 0., 0., 0.],
       [0., 1., 0., 0., 0.],
       [0., 0., 1., 0., 0.],
       [0., 0., 0., 1., 0.],
       [0., 0., 0., 0., 1.]])

# empty((행, 열)) : 초기화 없이 기존 메모리 값이 들어감
arr_empty = np.empty((3,3))
arr_empty

>>>
array([[6.94648543e-310, 3.27606076e-316, 6.94643909e-310],
       [6.94648032e-310, 6.94643909e-310, 2.42092166e-322],
       [6.94648543e-310, 6.94648543e-310, 3.28606460e-316]])

# like(배열) 지정한 배열과 동일한 shape의 행열을 만듦
# 종류 : np.zeros_like(), np.ones.like(), np.full_like(), np.empty_like()

arr_sample = np.array([[1, 2, 3], [4, 5, 6]])
arr_like = np.ones_like(arr_sample)
arr_like

>>>
array([[1, 1, 1],
       [1, 1, 1]])

배열 데이터 생성 함수

import numpy as np

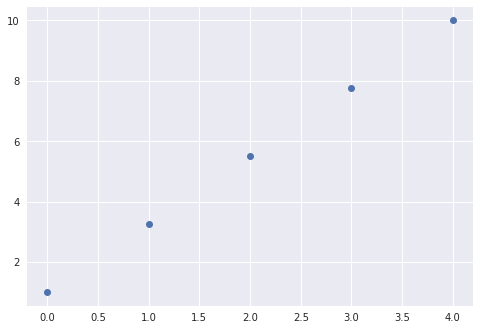
# np.linspace(시작, 종료, 개수) : 개수에 맞게끔 시작과 종료 사이에 균등하게 분배
arr_linspace = np.linspace(1, 10, 5)
arr_linspace

>>>
array([ 1.  ,  3.25,  5.5 ,  7.75, 10.  ])

import numpy as np
import matplotlib.pyplot as plt
plt.plot(arr_linspace, 'o') # 그래프를 그려주는 함수 마커를 원('o')으로
plt.show() # 만든 그래프를 보여줌

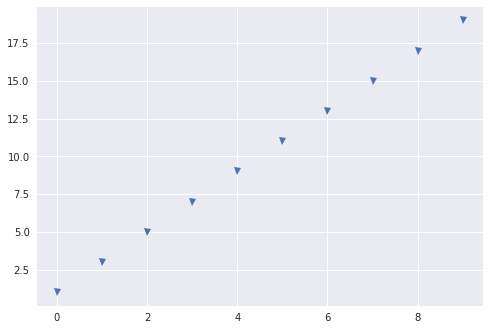
# np.arange(시작, 종료, 스텝) : 시작과 종료 사이에 스텝 간격으로 생성
arr_arange = np.arange(1, 20, 2)
arr_arange

>>>
array([ 1,  3,  5,  7,  9, 11, 13, 15, 17, 19])

plt.plot(arr_arange, 'v')
plt.show()

난수 기반 배열 생성

# np.random.normal(정규분포 평균, 표준편차, (행, 열) or 개수) : 정규 분포 확률 밀도에서 표본 추출

mean = 0 # 평균
std = 1 # 표준편차
arr_normal = np.random.normal(mean, std, 5)
arr_normal

>>> array([-0.04961036, -0.16293818, -1.35516979,  1.78376722, -1.19296801])

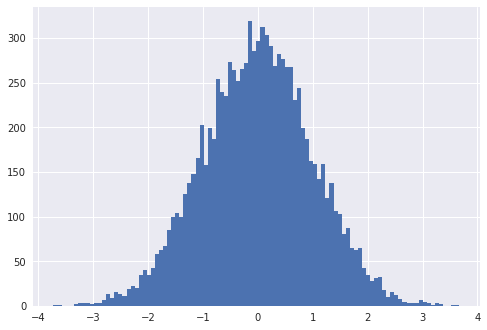
mean = 0 # 평균
std = 1 # 표준편차
data = np.random.normal(mean, std, 10000)
plt.hist(data, bins=100) # 나누는 구간 개수 (100개 정도로 더 잘게 나누어 보라는 의미)
plt.show()

# np.random.rand(행, 열 or 크기) : 행:열 또는 크기 만큼의 균등한 비율로 난수(0~1 사이) 생성
arr_rand = np.random.rand(3, 2)
arr_rand

>>>
array([[0.92676941, 0.15885109],
       [0.93533541, 0.64427414],
       [0.37361776, 0.52256276]])

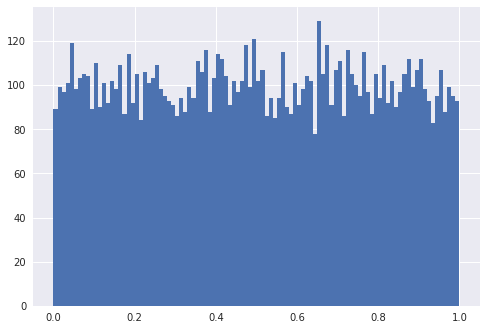
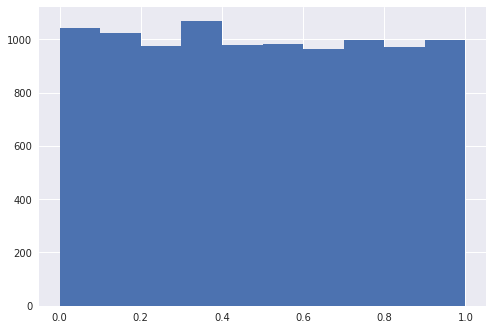
data = np.random.rand(10000)
plt.hist(data, bins=10) # 10개의 구간으로 나누어 히스토 그램을 보이라는 의미
plt.show()

# np.random.randn(행, 열 or 크기) : 기댓값이 0이고 표준편차가 1인 가우시안 표준 정규 분포를 따르는 난수를 생성
arr_randn = np.random.randn(3, 2)
arr_randn

>>>
array([[-1.3851809 , -1.55881959],
       [-1.40911545,  1.33672411],
       [ 0.44530289,  1.46332848]])

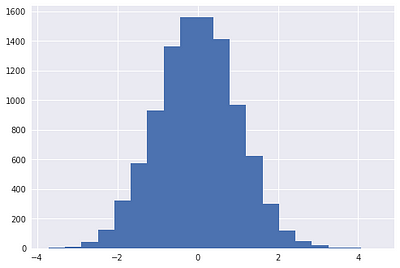
data = np.random.randn(10000)
plt.hist(data, bins=20) # 20개의 구간으로 나누어 히스토그램을 보이라는 의미
plt.show()

# np.random.randint(최소, 최대, size=(행, 열) or 크기) : 행:열 만큼의 정규 분포로 난수(최소~최대 사이) 생성
arr_randint = np.random.randint(10, 20, size=(3, 2))
arr_randint

>>>
array([[16, 18],
       [11, 14],
       [18, 16]])

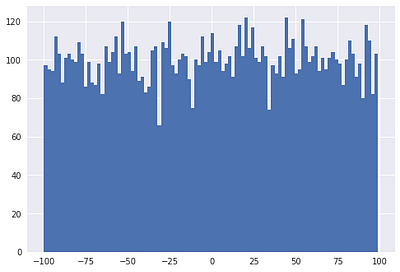
data = np.random.randint(-100, 100, 10000)
plt.hist(data, bins=100) # 100개의 구간으로 나누어 히스토 그램을 보이라는 의미
plt.show()

# np.random.random((행, 열) or 크기) : 행:열 만큼의 정류 분포로 난수(0~1 사이) 생성
arr_random = np.random.random((3, 2))
arr_random

>>>
array([[0.1714475 , 0.26868344],
       [0.03436504, 0.84737984],
       [0.22159394, 0.59953792]])

data = np.random.random(10000)
plt.hist(data, bins=100) # 100개의 구간으로 나누어 히스토 그램을 보이라는 의미
plt.show()